Что если определитель равен 0. Если определитель матрицы равен нулю, то обратная к ней не существует
Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения.
Определение 14.9 Квадратную матрицу назовем вырожденной или особенной матрицей , если , и невырожденной или неособенной матрицей , если .
Предложение 14.21 Если обратная матрица существует, то она единственна.
Доказательство . Пусть две матрицы и являются обратными для матрицы . Тогда
Следовательно, .
Правило Крамера .
Пусть матричное уравнение AX = B
Где ; – определитель, полученный из определителя D заменой i -го столбца столбцом свободных членов матрицы B :
 |
Доказательство теоремы разобъем на три части:
1.Решение системы (1) существует и является единственным.
2.Равенства (2) являются следствием матричного уравнения (1).
3.Равенства (2) влекут за собой матричное уравнение (1).
Так как , то существует и при том единственная, обратная матрица .
Умножая обе части матричного уравнения (1) слева на , получаем решение этого уравнения:
Единственность обратной матрицы доказывает первую часть теоремы.
Перейдем к доказательству взаимно-однознаяного соответствия между формулами (1) и (2).
Используя формулу (4), получим выражение для i -го элемента. Для этого нужно умножить i -ую строку матрицы
![]()
на столбец B .
Учитывая, что i -ая строка присоединенной матрицы составлена из алгебраических дополнений , получаем следующий результат:
Вывод формул Крамера завершен. Покажем теперь, что выражения
Изменим порядок суммирования в правой части полученного выражения:
где – дельта символ Кронекера.
Учитывая, что дельта символ снимает суммирование по одному из индексов, получаем требуемый результат:
Комплексные числа : Идея – определение новых объектов с помощью известных. Вещественные числа расположены на прямой. При переходе на плоскость получаем комплексные числа. Определение : Комплексным числом называется пара вещественных чисел z = (a,b). Число a = Re z называется вещественной частью, а b = Im z мнимой частью комплексного числа z .
Операции над комплексными числами: Комплексные числа z1 z2 равны Z1 = z2 ⇔ Re z1 = Re z2 & Im z1 = Im z2. Сложение: Z=z1+z2. ⇔Re z=Re z1+Re z2 & Im z1+ Im z2. Число (0,0) обозначается через 0. Это нейтральный элемент. Проверяется, что сложение комплексных чисел обладает свойствами аналогичными свойствам сложения вещественных чисел. (1. Z1+ z2 = z2 + z1 – коммутативность; 2. Z1 + (z2 + z3) = (z1 + z2) + z3 – ассоциативность; 3. Z1 + 0 = z1 - существование нуля (нейтрального элемента) ;4. z + (−z) = 0 - существование противоположного элемента). Умножение : z= z1 z2⇔Re z=Re z1 Re z2-Im z1 Im z2 & Im z1=Im z1 Re z2+Im z2 Re z1. Комплексное число z лежит на вещественной оси, если Imz = 0 . Результаты операций над такими числами совпадают с результатами операций над обычными вещественными числами. Умножение комплексных чисел обладает свойствами замкнутости, коммутативности и ассоциативности. Число (1,0) обозначается через 1. Оно является нейтральным элементом по умножению.Если a∈ R, z ∈C , то Re(az) = aRe z, Im(az) = a Imz . Определение Число (0,1) обозначается через i и называется мнимой единицей. В этих обозначениях получаем запись комплексного числа в алгебраической форме: z = a + ib, a,b∈ R. i=-1. (a,b)=(a,0)+(0,b) ;(a,0)+b(0,1)=a+ib=z; (a1+ib)(a2+ib2)=a1a2+i(a1b2+1-a2b1)-b1b2; (a+ib)(1+0i)=a+ib; z(a,b), z(0+i0)=0; z!=0; a 2 +b 2 >0 (a+ib)(a-ib/a 2 +b 2)=1.Число называется сопряженным к z, если Re =Re z ; Im =- Im z.
= + ; = ; z =(a+ib)(a-ib)=a 2 +b 2 Модулем числа z называется вещественное число| z |= . Справедлива формула| z| 2 = z Из определения следует, что z ≠ 0⇔| z|≠ 0. z -1 = /|z| 2 (1)
Тригонометрическая форма комплексного числа: a=r cos(t); b=r sin(t). Z=a+ib=r(cos(t)+isin(t)) (2) t-аргумент комплексного числа. Z1=z2 =>|z1|=|z2|
arg(z1)-arg(z2)=2пk.
Z1=r1(cos(t1)+isin(t1), Z2=r2(cos(t2)+isin(t2)), Z3=z1 z2=T1T2(cos(t1+t2)+isin(t1+t2)(1)
Arg(z1z2)=arg(z1)+arg(z2) (2)
Z!=0 z -1 = /|z| 2 =1/r(cos(-t)+i(sin(-t)) Z=r(cos(t)+istn(t))
R(cos(t)-isin(t))
Определение: Корнем степени n из единицы называются решения уравнения z n =1Предложение. Имеется n различных корней степени n из единицы. Они записываются в виде z = cos(2 π k / n) + isin(2 π k / n), k = 0,..., n −1 .Теорема. В множестве комплексных чисел уравнение всегда имеет n решений.Z=r(cos(t)+isin(t)); z n =r n (cos(nt)+isin(nt))=1(cos(0)+isin(0))=>z n =1 .Z-целые числа. K пренадлежит Z. k=2=E 2 =E n-1 E n ; E n =1; E n+p =E p . Таким образом доказано, что решениями уравнения являются вершины правильного n-угольника, причем одна из вершин совпадает с 1.
Корень n-ой степени из z 0 . Z k =Z 0 ; Z 0 =0=>Z=0; Z 0 !=0;Z=r(cos(t)-isin(t)); Z 0 =r 0 (cos(t0)+isin(t0)); r0!=0; Z n =r n (cos(nt)+isin(nt))
r n =r 0, nt-t 0 =2пk; r= ; t=(2пk+t0)/n; z= (cos((2пk+t0)/n)+isin((2пk+t0)/n)= (cos t0/n+isin t0/n)(cos(2пk/n)+isin(2пk/n))=Z 1 E k ; z=z 1 E k ; Z 1 n =z 0, k=0, n=1
Матрицы. Определение: Матрицей размера m × n называется прямоугольная таблица, содержащая m строк и n столбцов, элементы которой являются вещественными или комплексными числами. Элементы матрицы имеют двойные индексы.
Если m = n , то это квадратная матрица порядка m , а элементы с одинаковыми индексами образуют главную диагональ матрицы.
Операции над матрицами: Определение: Две матрицы A,B называются
равными, если их размеры совпадают и A = B,1≤ i ≤ m,1≤ j ≤ n
Сложение. Рассматриваются матрицы одного размера. Определение :C = A + B ⇔ C = A + B, ∀i, j Предложение . Сложение матриц коммутативно, ассоциативно, существует нейтральный элемент и для каждой матрицы существует противоположный элемент.
Нейтральным элементом является нулевая матрица, все элементы которой равны 0. Она обозначается через Θ.
Умножение. Матрица A размера m × n обозначается через Amn. Определение: С mk =A mn B nk ó
C= Заметим, что в общем случае умножение не является коммутативным. Замкнутость справедлива для квадратной матрицы фиксированного размера. Пусть даны три матрицы Amn , Bnk , Ckr . Тогда (AB)C = A(BC). Если произведение 3 матриц существует, то оно является ассоциативным.
Символ Кронекера δij . Он равен 1, если индексы совпадают, и 0 иначе. Определение. Единичной матрицей I n называется квадратная матрица порядка n , для которой выполнены равенства n I n [ i | j] = δ ij Предложение. Справедливы равенства I m A mn =A mn I n =A mn
Сложение и умножение матриц связанно законами дистрибутивности. A(B+C)=AB+AC; (A+B)C=AC+BC;(A(B+C)= = = +
Транспонирование матрицы. Транспонированная матрица - это матрица, полученная из исходной путем замены строк на столбцы.
(A+B) Т =А Т +В Т
(АВ) Т =В Т А Т;(AB) Т =(AB)= = (В Т А Т)
Умножение матрицы на число. Произведение числа а на матрицу A mn называется новая матрица B=aA
1*A=A;a(A+B)=aA+aB;(a+b)A=aA+bA;
A(BC)=(aB)C=B(aC); (ab)A=a(bA)=b(aA)
Линейным пространством (L) над полем F называется множество векторов L={α,β..}
1.α+β=β+α(коммутативность) 2.α+(β+γ)= (α+β)+γ, (ab)α=a(bα)(ассоциативность) 3.α+θ=α, α∙1=α(существование нейтрального) 4.α+(-α)=θ (существование противоположного)
a(α+β)=aα+aβ, (a+b)α=aα+bα. Док-во {|(a+b)α|=|a+b||α|, |aα|=|a||α|,|bα|=|b||α|, a и b>0, |a+b|=a+b,|a|=a,|b|=b.} aα+(-a)α=θ, (a+0)α=aα
Примером линейного пространства является множество матриц фиксированного размера с операциями сложения и умножения на число.
Система линейных векторов называется линейно зависимой , если 1.a 1 ,a 2 ..a n ≠0 2. a 1 α 1 ,a 2 α 2 ..a n α n =θ Если система не является линейно зависимой, то она линейно независима. Рассмотрим 1. n=1 α 1 завис. a 1 ≠0, a 1 α 1 =θ, a 1 -1 (a 1 α 1)= a 1 -1∙ θ=θ, (a 1 -1 a 1)α 1 =1∙α 1 =α 1 ; 2. n=2 α 1 ,α 2 завис. a 1 ≠0 ,a 1 α 1 +a 2 α 2 =θ ,α 1 = -a 1 -1 a 2 α 2 =b 2 α 2; 3.n≥2 α 1 ..α n завис. a 1 ≠0, α 1 =Σ k =2 n b k α k , 1α 1 - Σ k =2 n b k α k =θ, (1,b 2 ..b n)≠0
Предложение : Система векторов, содержащая более чем 1 вектор линейно зависима ттогда какой-то вектор системы есть линейная комбинация остальных.
Если система векторов содержит линейно зависимую подсистему, то вся система линейно зависима. Док-во: {α 1 ..α n завис. Система: α 1 ..α n ;α n +1 ..α m , a 1 α 1 +..+a n α n +0α n +1 +..+0α m =θ, a 1 ..a n ,0..0≠0.} Если система содержит нул.вектор, то она линейно зависима. Теорема о линейных пространствах : {Пусть даны 2 системы векторов α 1 ..α m , β 1 ..β n . Система векторов α выражается через β, если каждый вектор α есть линейная комбинация β α i = Σ k =1 n a ik β k , (α) { (β), (β) { (γ)→ (α) { (γ)} Теорема: Даны 2 системы векторов, при этом α независимая и, (α) { (β)→m≤n Докажем, α 1 ..α m +1 β 1 ..β m (α) { (β)→(α)завис. {Докажем методом индукции. m=1: α 1 =a 11 β 1 , α 2 =a 21 β 1 . a 11 =0→ α 1 =θ. a 11 α 2 – a 21 α 1 = a 11 a 21 β 1 - a 21 a 11 β 1 =θ. α 1 = a 11 β 1 +.. a 1 n -1 β n -1 .. α n = a n 1 β 1 +.. a nn -1 β n -1 Если все коэффициенты =0 a 11 =a 12 =..=a 1 n -1 =0→ α 1 =θ→ вся система линейно зависима. a 1 n -1 ≠0 α 2 ′= α 2 –с 2 α 1 =b 21 β 1 +..+b 2 n -2 β n -2 , c 2 =a 2 n -1 / a 1 n -1 , α 3 ′= α 3 –с 3 α 1 .. α n ′= α n –с n α 1 . По пред. индукции сущ-ет ненулевой набор чисел d 2 ..d n: d 2 α 2 ′+d 3 α 3 ′+.. d n α n ′=θ , d 2 (α 2 –с 2 α 1)+d 3 (α 3 –с 3 α 1)+.. d n (α n –с n α 1)=θ , (α) { (β), m>n →(α)завис. если (α) независ. →m≤n}
МЛНП -макс.лин.незвавис.подсистемы. Пусть дана система векторов α 1 ..α n некоторой подсис. α i 1 ..α in называется МЛНП, если 1. α 1 ..α n независ.2. α i 1 ..α ir , α ij завис. Каждый вектор системы есть линейная комбинация векторов МЛНП. { α i 1 ..α ir , α ij завис. a i 1 α i 1 +.. a ir α ir +a ij α ij =θ
a i 1 ..a ir , a ij ≠0 если a ij =0 → a i 1 α i 1 +.. a ir α ir =θ a i 1 ..a ir =0 противоречие a ij ≠0 α ij = a ij -1 (-a i 1 α i 1 -.. a ir α ir) (α 1 ..α n) { (α i 1 ..α ir)
Следствие : Любые 2 МЛНП из одной системы векторов содержат одинаковое число векторов (α i 1 ..α ir) { (α j 1 ..α jk) , (α j 1 ..α jk) { (α i 1 ..α ir) k≤r, r≤k →r=k Число векторов МЛНП называется рангом исходной системы. В случае линейного пространства(система векторов состоит из всех векторов пространства) МЛНП мб конечна или бесконечна. Рассматриваем конечный случай. Число векторов(ранг)- размерность линейного пространства. МЛНП-база. Пространство направленных отрезков. Два неколлинеарных вектора составляют базу в пространстве векторов на плоскости. α 3 = α 1 ′+ α 2 ′=a 1 α 1 + a 2 α 2 . 3 вектора линейно зависимые α 3 =a 1 α 1 + a 2 α 2 . Компланарность- 3 вектора параллельны одной плоскости α 4 = α 4 ′+ α 5 ′ , α 4 ′=a 1 α 1 + a 2 α 2 , α 5 ′= a 3 α 3 , α 4 = a 1 α 1 + a 2 α 2 + a 3 α 3 . Пространство строк длины n . α= Предложение: Пространство строк длины n имеет размерность n. { ξ 1 =<1…0> ξ 2 =<0,1…0> .. ξ n =<0…1> ,a 1 ξ 1 + a 2 ξ 2 +.. a n ξ n =θ=<0,..0> → a 1 =a 2 =..a n =0 (линейная независимость) β= β= b 1 ξ 1 + b 2 ξ 2 +.. b n ξ n →пространство строк длины n имеет размерность и n.
Ранг матрицы.
Две системы векторов α и β называются эквивалентными, если каждый вектор
α{ β(выражается) и β{ α.
Предложение. Ранги эквивалентных систем совпадают.
α i 1 , α i 2 ,…, α ir – МЛНП α , β i 1 , β i 2 ,…, β ik – МЛНП β , α i 1 , α i 2 ,…, α ir < β < β i 1 , β i 2 ,…, β ik → r<=k
Поменяв местами α и β местами → r>=k >>> Значит, r=k.
Определение. Пусть дана матрица A=
Рангом матрицы А называется ранг системы векторов α1, α2,…, αm, составленных из это матрицы >>rank(A)-ранг
Из определения очевидно, что при перестановке столбцов ранг не меняется. Покажем, что при перестановке столбцов ранг так же не меняется.
А’= 
Линейно зависимы:
b 1 α 1 + b 2 α 2 +…+ b m α m =θ, b 1 а 11 +b 2 a 21 +…+b m a m 1=0, b 1 α’ 1 + b 2 α’ 2 +…+ b m α’ m , b 1 а 11 +b 2 a 21 +…+b m a m 1=0
2.Если │А│=0, то матрица А вырожденная и обратной матрицы А -1 не существует.
Если определитель матрицы А не равен нулю, то обратная матрица существует.
3. Находим А T , транспонированную к А.
4. Находим алгебраические дополнения элементов транспонированной матрицы и составляем из них присоединенную матрицу. 5. Вычисляем обратную матрицу по формуле: 6. Проверяем правильность вычисления обратной матрицы, исходя из её определения А -1 ∙А = А ∙А -1 = Е.
· №28
· В матрице размера m x n вычеркиванием каких-либо строк и столбцов можно выделить квадратные подматрицы k-го порядка, где k≤min(m; n). Определители таких подматриц называются минорами k-го порядка матрицы А.
· Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.
· Ранг матрицы А обозначается rang A или r(A).
· Из определения следует:
· 1) ранг матрицы размера m x n не превосходит меньшего из её размеров, т.е. r(A) ≤ min (m; n).
· 2) r(A)=0 тогда и только тогда, когда все элементы матрицы равны нулю, т.е. А=0.
· 3) Для квадратной матрицы n-го порядка r(A) = n тогда и только тогда, когда матрица А – невырожденная.
· В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются элементарные преобразования, сохраняющие ранг матрицы:
· 1) Отбрасывание нулевой строки (столбца).
· 2) Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
· 3) Изменение порядка строк (столбцов) матрицы.
· 4) Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
· 5) Транспонирование матрицы.
· Теорема. Ранг матрицы не изменится при элементарных преобразованиях матрицы.
№31
Пусть число уравнений системы (1) равно числу переменных, т.е. m=n. Тогда матрица системы является квадратной, а её определитель Δ=│А│называется определителем системы.
Предположим, что │А│не равен нулю, тогда существует обратная матрица А -1 .
Умножая слева обе части матричного равенства на обратную матрицу А -1 получим:
А -1 (АХ)= А -1 В.
Решением системы уравнений методом обратной матрицы будет матрица-столбец:
Х= А -1 В.
(А -1 А)Х =ЕХ =Х
 Теорема Крамера. Пусть Δ – определитель матрицы системы А, а Δ j – определитель матрицы, полученный из матрицы заменой j-го столбца столбцом свободных членов. Тогда если Δ не равен нулю, то система имеет единственное решение, определённое по формулам Крамера:
Теорема Крамера. Пусть Δ – определитель матрицы системы А, а Δ j – определитель матрицы, полученный из матрицы заменой j-го столбца столбцом свободных членов. Тогда если Δ не равен нулю, то система имеет единственное решение, определённое по формулам Крамера:
 где j=1..n.
где j=1..n.
№33
 Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого или треугольного вида.
Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого или треугольного вида.
Рассмотрим матрицу:
эта матрица называется расширенной матрицей системы (1), так как в нее кроме матрицы системы А, дополнительно включен столбец свободных членов.
№26
N-мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде Х=(х 1 ,х 2 ,…х n) , где х i – i-я компонента вектора Х.
Два n-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е. Х=У, если x i =y i , i=1…n.
Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие приведённым выше свойствам, называется векторным пространством.
Векторное пространство R, называется n-мерным, если в нем существует n линейно независимых векторов, а любые n+1 векторов уже являются зависимыми. Число n называется размерностью векторного пространство R и обозначается dim(R).
№29
Линейные операторы
Определение. Если задан закон (правило), по которому каждому вектору x пространства ставится в соответствие единственный вектор y пространства
то говорят: что задан оператор (преобразование, отображение) A(x), действующий из в и
записывают y=A(x).
Оператор называется линейным, если для любого вектора x и y пространства
 и любого числа λ выполняются следующие соотношения:
и любого числа λ выполняются следующие соотношения:
№37
Пустъ А – множество, состоящее из конечного числа элементов a 1 , a 2, a 3 …a n . Из различных элементов множества А можно образовывать группы. Если в каждую группу входит одно и то же число элементов m (m из n), то говорят, что они образуют соединения из n элементов пo m в каждом. Различают три вида соединений: размещения, сочетания и перестановки.
Соединения, в каждое из которых входят все n элементов множества А и которые, следовательно, отличаются друг от друга только порядком элементов называются перестановками из n элементов. Число таких перестановок обозначается символом Р n .
№35
Классическое определение вероятности основано на понятии равновозможности событий.
Равновозможность событий означает, что нет оснований предпочесть какое-либо одно из них другим.
Рассмотрим испытание, в результате которого может произойти событие A. Каждый исход, при котором осуществляется событие A, называется благоприятным событию A.
Вероятностью события A (обозначают P(A)) называется отношение числа исходов, благоприятных событию A (обозначают k), к числу всех исходов испытания – N т.е. P(A)= k/ N.
Из классического определения вероятности вытекают следующие ее свойства:
Вероятность любого события заключена между нулем и единицей.
Вероятность достоверного события равна единице.
Вероятность невозможного события равна нулю
№39, 40
 Теорема сложения. Если А и В несовместны, то Р(А + В) = Р(А) +Р(В)
Теорема сложения. Если А и В несовместны, то Р(А + В) = Р(А) +Р(В)
Система называется однородной, если в ней все свободные члены равны нулю. Если такая однородная система имеет характеристические определители, то их последний столбец состоит из нулей, и они все равны нулю. Совершенно очевидно, что всякая однородная система имеет решение
которое в дальнейшем мы будем называть нулевым.
Для однородной системы основным является вопрос о том, имеет ли она решения, отличные от нулевого, и если имеет, то какова будет совокупность всех таких решений. Рассмотрим сначала тот случай, когда число уравнений равно числу неизвестных. Система будет иметь вид:

Если определитель этой системы отличен от нуля, то, согласно теореме Крамера, эта система имеет одно определенное решение, а именно в данном случае нулевое решение. Если же этот определитель равен нулю, то ранг k таблицы коэффициентов будет меньше числа неизвестных и, следовательно, значения (п - k) неизвестных останутся совершенно произвольными, и мы будем иметь бесчисленное множество решений, отличных от нулевого. Мы приходим таким образом к следующей основной теореме:
Теорема I. Для того чтобы система (14) имела решение, отличное от нулевого, необходимо и достаточно, чтобы ее определитель равнялся нулю.
Проведем параллель тех результатов, которые мы получили для неоднородной системы (1) и однородной системы (14). Если определитель системы отличен от нуля, то неоднородная система (1) имеет одно определенное решение, и однородная система - только нулевое решение. Если же определитель системы равен нулю, то однородная система (14) имеет решения, отличные от нулевого, но при этом условии неоднородная система (1), вообще говоря, вовсе решения не имеет, ибо для того, чтобы она имела решение, необходимо, чтобы свободные ее члены были выбраны так, чтобы они обращали в нуль все характеристические определители. Приведенный параллелизм результатов будет играть в дальнейшем существенную роль. В вопросах физики однородные системы встретятся при рассмотрении собственных колебаний, а неоднородные - при рассмотрении вынужденных колебаний, и указанный выше случай равенства нулю определителя будет характеризовать для однородной системы наличие собственных колебаний, а для неоднородной системы - явление резонанса.
Переходим теперь к более подробному рассмотрению решений системы (14), когда ее основной определитель равен нулю. Пусть k есть ранг таблицы ее коэффициентов, причем, очевидно, . Согласно доказанной в предыдущем номере теореме, мы должны взять те k уравнений, которые содержат главный определитель, и решить их относительно k неизвестных.
Положим, не ограничивая общности, что эти неизвестные будут . Решения получатся в виде:
где определенные численные коэффициенты и могут принимать произвольные значения.
Отметим одно общее свойство решения системы (14), непосредственно вытекающее из линейности и однородности этой системы, и которое может быть названо принципом наложения решений, а именно - если мы имеем несколько решений системы:
то, умножая их на произвольные постоянные и складывая, мы получим также решение системы
Поступая аналогично тому, как это мы делали для линейных дифференциальных уравнений , назовем решения (16) линейно-независимыми, если не существует никаких значений постоянных Q, среди которых есть отличные от нуля, таких, что при всяком s имеют место равенства:

Нетрудно построить линейно-независимых решений системы таких, что, умножая их на произвольные постоянные и складывая, получим все решения системы. Действительно, обратимся к формулам (15), дающим общее решение системы, и построим на основе этих формул решения следующим образом: в первом решении положим а все остальные равными нулю; во втором решении положим а все остальные равными нулю и т. д. и, наконец, в последнем решении положим и все остальные равными нулю. Нетрудно видеть, что построенные решения линейно-независимы, так как каждое из них содержит одно из неизвестных равным единице, которое в остальных решениях равно нулю. Обозначим полученные решения следующим образом.
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
 ;
;
 .
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:


Итак, решение системы (2):
онлайн-калькулятором , решающим методом Крамера.
Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
** ![]() ,
,
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет
(система несовместна)
Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
 .
.
На основании теоремы Крамера
………….
,
где -
-
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:
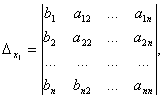


Пример 2.
 .
.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители


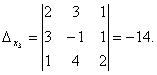
По формулам Крамера находим:
![]()
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
 .
.
Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных



По формулам Крамера находим:
Итак, решение системы - (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных


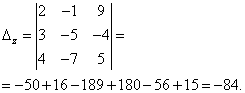
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных - буквы. За примерами далеко ходить не надо.
Следующий пример - на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных
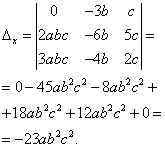
 Ферментативных реакций кинетика
Ферментативных реакций кинетика Ряд лигандов по силе. Модели химической связи. Теория кристаллического поля. Обзор теории кристаллического поля
Ряд лигандов по силе. Модели химической связи. Теория кристаллического поля. Обзор теории кристаллического поля Термодинамические потенциалы
Термодинамические потенциалы