Непрерывная функция в точке. Непрерывность функций – теоремы и свойства. Установить непрерывность функции в точке самостоятельно, а затем посмотреть решение

1. Введение.

2. Определение непрерывности функции.

3. Классификация точек разрыва

4. Свойства непрерывных функций.

6. Заключение.

10.1. Введение

Всякий раз, оценивая неизбежные с течением времени изменения в окружающем нас мире, мы пытаемся проанализировать происходящие процессы, чтобы выделить их наиболее существенные черты. Один из первых на этом пути встает вопрос: как происходят характерные для этого явления изменения – непрерывно или дискретно , т.е. скачкообразно. Равномерно ли понижается курс валюты или обваливается, происходит постепенная эволюция или революционный скачок? Чтобы унифицировать качественные и количественные оценки происходящего, следует абстрагироваться от конкретного содержания и изучить проблему в терминах функциональной зависимости. Это позволяет сделать теория пределов, которую мы рассматривали на прошлой лекции.

10.2. Определение непрерывности функции

Непрерывность функции интуитивно связано с тем, что ее графиком является сплошная, нигде не прерывающаяся кривая. Мы вычерчиваем график такой функции, не отрывая ручки от бумаги. Если функция задана таблично, то о ее непрерывности, строго говоря, судить нельзя, потому что при заданном шаге таблицы поведение функции в промежутках не определено.

В реальности при непрерывности имеет место следующее обстоятельство: если параметры, характеризующие ситуацию, немного изменить, то не много изменится и ситуация. Здесь важно не то, что ситуация изменится, а то, что она изменится «немного».

Сформулируем понятие непрерывности на языке приращений. Пусть некоторое явление описывается функцией и точка a принадлежит области определения функции. Разность называется приращением аргумента в точке a , разность – приращением функции в точке a .

Определение 10.1. Функция непрерывна в точке a, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции :

Пример 10.1. Исследовать на непрерывность функцию в точке .

Решение. Построим график функции и отметим на нем приращения Dx и Dy (рис. 10.1).

Из графика видно, что чем меньше приращение Dx , тем меньше Dy . покажем это аналитически. Приращение аргумента равно , тогда приращение функции в этой точке будет равно

Отсюда видно, что если , то и :

Дадим еще одно определение непрерывности функции.

Определение 10.2. Функция называется непрерывной в точке а, если:

1) она определена в точке а, и некоторой ее окрестности;

2) односторонние пределы существуют и равны между собой:

;

3) предел функции при х ®а равен значению функции в этой точке:

Если хотя бы одно из этих условий нарушается, то говорят, что функция претерпевает разрыв .

Это определение является рабочим для установления непрерывности в точке. Следуя его алгоритму и отмечая совпадения и несовпадения требований определения и конкретного примера, можно сделать вывод о непрерывности функции в точке.

В определении 2 четко проступает идея близости, когда мы вводили понятие предела. При неограниченном приближении аргумента x к предельному значению a , непрерывная в точке a функция f (x ) сколь угодно близко приближается к предельному значению f (a ).

10.3. Классификация точек разрыва

Точки, в которых нарушаются условия непрерывности функции, называются точками разрыва этой функции. Если x 0 – точка разрыва функции , в ней не выполняется, по крайней мере, одно из условий непрерывности функции. Рассмотрим следующий пример.

1. Функция определена в некоторой окрестности точки a , но не определена в самой точке a . Например, функция не определена в точке a =2, поэтому претерпевает разрыв (см. рис. 10.2).

Рис. 10.2 Рис. 10.3

2. Функция определена в точке a и в некоторой ее окрестности, ее односторонние пределы существуют, но не равны другу:, то функция претерпевает разрыв. Например, функция

определена в точке , однако при функция испытывает разрыв (см. рис. 10.3), т.к.

и ().

3. Функция определена в точке a и в некоторой ее окрестности, существует предел функции при , но этот предел не равен значению функции в точке a :

Например, функция (см. рис. 10.4)

Здесь – точка разрыва:

Все точки разрыва делятся на точки устранимого разрыва, точки разрыва первого и второго рода.

Определение 10.1. Точка разрыва называется точкой устранимого разрыва , если в этой точке существуют конечные пределы функции слева и справа, равные друг другу:

Предел функции в этой точке существует, но не равен значению функции в предельной точке (если функция определена в предельной точке), или функция в предельной точке не определена.

На рис. 10.4 в точке условия непрерывности нарушены, и функция имеет разрыв. На графике точка (0; 1) выколота . Впрочем, этот разрыв легко устранить – достаточно переопределить данную функцию, положив ее равной своему пределу в этой точке, т.е. положить . Поэтому такие разрывы называются устранимыми.

Определение 10.2. Точка разрыва называется точкой разрыва 1-го рода , если в этой точке существуют конечные пределы функции слева и справа, но они не равны друг другу:

Говорят, что в этой точке функция испытывает скачок .

На рис. 10.3 функция имеет разрыв 1-го рода в точке . Пределы слева и справа в этой точке равны:

и .

Скачок функции в точке разрыва равен .

Доопределить такую функцию до непрерывной невозможно. График состоит из двух полупрямых, разделенных скачком.

Определение 10.3. Точка разрыва называется точкой разрыва 2-го рода , если, по крайней мере, один из односторонних пределов функции (слева или справа) не существуют или равны бесконечности.

На рис 10.3 функция в точке имеет разрыв 2-го рода. Рассмотренная функция при является бесконечно большой и конечного предела ни справа, ни слева не имеет. Поэтому говорить о непрерывности в такой точке не приходится.

Пример 10.2. Построить график и определить характер точек разрыва:

Решение. Построим график функции f (x ) (рис 10.5).

Из рисунка видно, что исходная функция имеет три точки разрыва: , x 2 = 1,
x 3 = 3. Рассмотрим их по порядку.

Поэтому точке имеется разрыв 2-го рода .

а) Функция определена в этой точке: f (1) = –1.

б) , ,

т.е. в точке x 2 = 1 имеется устранимый разрыв . Переопределив значение функции в этой точке: f (1) = 5, разрыв устраняется и функция в этой точке становится непрерывной.

а) Функция определена в этой точке: f (3) = 1.

Значит, в точке x 1 = 3 имеется разрыв 1-го рода . Функция в этой точке испытывает скачок, равный Dy = –2–1 = –3.

10.4. Свойства непрерывных функций

Вспоминая соответствующие свойства пределов, заключаем, что функция, являющаяся результатом арифметических действий над непрерывными в одной и той же точке функциями, также непрерывны. Отметим:

1) если функции и непрерывны в точке a , то функции , и (при условии, что ) также непрерывны в этой точке;

2) если функция непрерывна в точке a и функция непрерывна в точке , то сложная функция непрерывна в точке a и

т.е. знак предела можно вносить под знак непрерывной функции.

Говорят, что функция непрерывна на некотором множестве, если она непрерывна в каждой точке этого множества . График такой функции – непрерывная линия, которая вычеркивается одним росчерком пера.

Все основные элементарные функции непрерывны во всех точках, где они определены .

Функции, непрерывные на отрезке , обладают рядом важных отличительных свойств. Сформулируем теоремы, выражающие некоторые из этих свойств.

Теорема 10.1 (теорема Вейерштрасса ). Если функция непрерывна на отрезке, то она на этом отрезке достигает своих наименьшего и наибольшего значений.

Теорема 10.2 (теорема Коши ). Если функция непрерывна на отрезке, то она на этом отрезке все промежуточные значения между наименьшим и наибольшим значениями .

Из теоремы Коши следует следующее важное свойство.

Теорема 10.3 . Если функция непрерывна на отрезке и на концах отрезка принимает значения разных знаков, то между a и b найдется такая точка c, в которой функция обращается в нуль: .

Геометрический смысл этой теоремы очевиден: если график непрерывной функции переходит с нижней полуплоскости на верхнюю (или наоборот), то по крайней мере в одной точке она пересечет ось Ox (рис.10.6).

Пример 10.3. Приближенно вычислить корень уравнения

, (т.е. приближенно заменить) многочленном соответствующей степени.

Это очень важное для практики свойство непрерывных функций. Например, очень часто непрерывные функции задаются таблицами (данными наблюдений или экспериментов). Тогда используя какой-либо метод можно таблично заданную функцию заменить многочленом. В соответствии с теоремой 10.3 это можно всегда сделать с достаточно высокой точностью. Работать с аналитически заданной функцией (тем более с многочленом) гораздо проще.

10.5. Экономический смысл непрерывности

Большинство функций, используемых в экономике, являются непрерывными и это позволяет высказывать вполне значимые утверждения экономического содержания.

В качестве иллюстрации рассмотрим следующий пример.

Налоговая ставка N имеет примерно такой график, как на рис. 10.7а.

На концах промежутков она разрывна и разрывы эти 1-го рода. Однако сама величина подоходного налога P (рис. 10.7б) является непрерывной функцией годового дохода Q . Отсюда, в частности, вытекает, что если годовые доходы двух людей различаются незначительно, то и различие в величинах подоходного налога, который они должны уплатить, также должны различаться не значительно. Интересно, что обстоятельство воспринимается огромным большинством людей как совершенно естественное, над которым они даже не задумываются.

10.6. Заключение

Под занавес позволим себе небольшое отступление.

Вот как можно графически выразить грустное наблюдение древних:

Sic transit Gloria mundi …

(Так проходит земная слава …)

Конец работы -

Эта тема принадлежит разделу:

Понятие функции

Понятие функции.. все течет и все меняется гераклит.. таблица х х х х y у у у у у..

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Непрерывная функция представляет собой функцию без «скачков», то есть такую, для которой выполняется условие: малым изменениям аргумента следуют малые изменения соответствующих значений функции. График подобной функции представляет из себя плавную или непрерывную кривую.

Непрерывность в точке, предельной для некоторого множества, можно определить с помощью понятия предела, а именно: функция должна иметь в этой точке предел, который равен ее значению в предельной точке.

При нарушении этих условий в некоторой точке, говорят, что функция в данной точке терпит разрыв, то есть ее непрерывность нарушается. На языке пределов точку разрыва можно описать как несовпадение значения функции в разрывной точке с пределом функции (если он существует).

Точка разрыва может быть устранимой, для этого необходимо существование предела функции, но несовпадающего с его значением в заданной точке. В этом случае ее в этой точке можно «поправить», то есть доопределить до непрерывности.
Совсем иная картина складывается, если предела функции в заданной существует. Возможно два варианта точек разрыва:

первого рода - имеются и конечны оба из односторонних пределов, и значение одного из них или обоих не совпадают со значением функции в заданной точке;
второго рода, когда не существует один или оба из односторонних пределов или их значения бесконечны.

Свойства непрерывных функций

Функция, полученная в результат арифметических действий, а также суперпозиции непрерывных функций на их области определения также является непрерывной.
Если дана непрерывная функция, которая положительна в некоторой точке, то всегда можно найти достаточно малую ее окрестность, на которой она сохранит свой знак.
Аналогично, если ее значения в двух точках A и B равны, соответственно, a и b, причем a отлично от b, то для промежуточных точек она примет все значения из промежутка (a ; b). Отсюда можно сделать интересное заключение: если дать растянутой резинке сжаться так, чтобы она не провисала (оставалась прямолинейной), то одна из ее точек останется неподвижной. А геометрически это означает, что существует прямая, проходящая через любую промежуточную точку между A и B, которая пересекает график функции.

Отметим некоторые из непрерывных (на области их определения) элементарных функций:

постоянная;
рациональная;
тригонометрические.

Между двумя фундаментальными понятиями в математике - непрерывностью и дифференцируемостью - существует неразрывная связь. Достаточно только вспомнить, что для дифференцируемости функции необходимо, чтобы это была непрерывная функция.

Если же функция в некоторой точке дифференцируема, то там она непрерывна. Однако совсем не обязательно, чтобы и ее производная была непрерывной.

Функция, имеющая на некотором множестве непрерывную производную, принадлежит отдельному классу гладких функций. Иначе говоря, это - непрерывно дифференцируемая функция. Если же производная имеет ограниченное количество точек разрыва (только первого рода), то подобную функцию называют кусочно гладкой.

Еще одним важным понятием является равномерная непрерывность функции, то есть ее способность быть в любой точке своей области определения одинаково непрерывной. Таким образом, это свойство, которое рассматривается на множестве точек, а не в какой-либо отдельно взятой.

Если же зафиксировать точку, то получится не что иное, как определение непрерывности, то есть из наличия равномерной непрерывности вытекает, что перед нами непрерывная функция. Вообще говоря, обратное утверждение неверно. Однако согласно теореме Кантора, если функция непрерывна на компакте, то есть на замкнутом промежутке, то она на нем равномерно непрерывна.

Определение
Функция f(x) называется непрерывной в точке x 0 окрестности этой точки, и если предел при x стремящемся к x 0 равен значению функции в x 0 :
.

Используя определения предела функции по Коши и по Гейне , можно дать развернутые определения непрерывности функции в точке .

Можно сформулировать понятие непрерывности в терминах приращений . Для этого мы вводим новую переменную , которая называется приращением переменной x в точке . Тогда функция непрерывна в точке , если
.
Введем новую функцию:
.
Ее называют приращением функции в точке . Тогда функция непрерывна в точке , если
.

Определение непрерывности справа (слева)
Функция f(x) называется непрерывной справа (слева) в точке x 0 , если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x 0 равен значению функции в x 0 :
.

Теорема об ограниченности непрерывной функции
Пусть функция f(x) непрерывна в точке x 0 . Тогда существует такая окрестность U(x 0) , на которой функция ограничена.

Теорема о сохранении знака непрерывной функции
Пусть функция непрерывна в точке . И пусть она имеет положительное (отрицательное) значение в этой точке:
.
Тогда существует такая окрестность точки , на которой функция имеет положительное (отрицательное) значение:
при .

Арифметические свойства непрерывных функций
Пусть функции и непрерывны в точке .
Тогда функции , и непрерывны в точке .
Если , то и функция непрерывна в точке .

Свойство непрерывности слева и справа
Функция непрерывна в точке тогда и только тогда, когда она непрерывна в справа и слева.

Доказательства свойств приводятся на странице «Свойства непрерывных в точке функций ».

Непрерывность сложной функции

Теорема о непрерывности сложной функции
Пусть функция непрерывна в точке . И пусть функция непрерывна в точке .
Тогда сложная функция непрерывна в точке .

Предел сложной функции

Теорема о пределе непрерывной функции от функции
Пусть существует предел функции при , и он равен :
.
Здесь точка t 0 может быть конечной или бесконечно удаленной: .
И пусть функция непрерывна в точке .
Тогда существует предел сложной функции , и он равен :
.

Теорема о пределе сложной функции
Пусть функция имеет предел и отображает проколотую окрестность точки на проколотую окрестность точки . Пусть функция определена на этой окрестности и имеет на ней предел .
Здесь - конечные или бесконечно удаленные точки: . Окрестности и соответствующие им пределы могут быть как двусторонние, так и односторонние.
Тогда существует предел сложной функции и он равен :
.

Точки разрыва

Определение точки разрыва
Пусть функция определена на некоторой проколотой окрестности точки . Точка называется точкой разрыва функции , если выполняется одно из двух условий:
1) не определена в ;
2) определена в , но не является в этой точке.

Определение точки разрыва 1-го рода
Точка называется точкой разрыва первого рода , если является точкой разрыва и существуют конечные односторонние пределы слева и справа :
.

Определение скачка функции
Скачком Δ функции в точке называется разность пределов справа и слева
.

Определение точки устранимого разрыва
Точка называется точкой устранимого разрыва , если существует предел
,
но функция в точке или не определена, или не равна предельному значению: .

Таким образом, точка устранимого разрыва - это точка разрыва 1-го рода, в которой скачек функции равен нулю.

Определение точки разрыва 2-го рода
Точка называется точкой разрыва второго рода , если она не является точкой разрыва 1-го рода. То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.

Свойства функций, непрерывных на отрезке

Определение функции, непрерывной на отрезке
Функция называется непрерывной на отрезке (при ), если она непрерывна во всех точках открытого интервала (при ) и в точках a и b , соответственно.

Первая теорема Вейерштрасса об ограниченности непрерывной на отрезке функции
Если функция непрерывна на отрезке , то она ограничена на этом отрезке.

Определение достижимости максимума (минимума)
Функция достигает своего максимума (минимума) на множестве , если существует такой аргумент , для которого
для всех .

Определение достижимости верхней (нижней) грани
Функция достигает своей верхней (нижней) грани на множестве , если существует такой аргумент , для которого
.

Вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции
Непрерывная на отрезке функция достигает на нем своих верхней и нижней граней или, что тоже самое, достигает на отрезке своего максимума и минимума.

Теорема Больцано - Коши о промежуточном значении
Пусть функция непрерывна на отрезке . И пусть C есть произвольное число, находящееся между значениями функции на концах отрезка: и . Тогда существует точка , для которой
.

Следствие 1
Пусть функция непрерывна на отрезке . И пусть значения функции на концах отрезка имеют разные знаки: или . Тогда существует точка , значение функции в которой равно нулю:
.

Следствие 2
Пусть функция непрерывна на отрезке . И пусть . Тогда функция принимает на отрезке все значения из и только эти значения:
при .

Обратные функции

Определение обратной функции
Пусть функция имеет область определения X и множество значений Y . И пусть она обладает свойством:
для всех .
Тогда для любого элемента из множества Y можно поставить в соответствие только один элемент множества X , для которого . Такое соответствие определяет функцию, которая называется обратной функцией к . Обратная функция обозначается так:
.

Из определения следует, что
;
для всех ;
для всех .

Лемма о взаимной монотонности прямой и обратной функций
Если функция строго возрастает (убывает) , то существует обратная функция , которая также строго возрастает (убывает).

Свойство о симметрии графиков прямой и обратной функций
Графики прямой и обратной функций симметричны относительно прямой .

Теорема о существовании и непрерывности обратной функции на отрезке
Пусть функция непрерывна и строго возрастает (убывает) на отрезке . Тогда на отрезке определена и непрерывна обратная функция , которая строго возрастает (убывает).

Для возрастающей функции . Для убывающей - .

Теорема о существовании и непрерывности обратной функции на интервале
Пусть функция непрерывна и строго возрастает (убывает) на открытом конечном или бесконечном интервале . Тогда на интервале определена и непрерывна обратная функция , которая строго возрастает (убывает).

Для возрастающей функции .
Для убывающей: .

Аналогичным образом можно сформулировать теорему о существовании и непрерывности обратной функции на полуинтервале.

Свойства и непрерывность элементарных функций

Элементарные функции и обратные к ним непрерывны на своей области определения. Далее мы приводим формулировки соответствующих теорем и даем ссылки на их доказательства.

Показательная функция

Показательная функция f(x) = a x , с основанием a > 0 - это предел последовательности
,
где есть произвольная последовательность рациональных чисел, стремящаяся к x :
.

Теорема. Свойства показательной функции
Показательная функция имеет следующие свойства:
(П.0) определена, при , для всех ;
(П.1) при a ≠ 1 имеет множество значений ;
(П.2) строго возрастает при , строго убывает при , является постоянной при ;
(П.3) ;
(П.3*) ;
(П.4) ;
(П.5) ;
(П.6) ;
(П.7) ;
(П.8) непрерывна для всех ;
(П.9) при ;
при .

Логарифм

Логарифмическая функция, или логарифм, y = log a x , с основанием a - это функция, обратная к показательной функции с основанием a .

Теорема. Свойства логарифма
Логарифмическая функция с основанием a , y = log a x , имеет следующие свойства:
(Л.1) определена и непрерывна, при и , для положительных значений аргумента,;
(Л.2) имеет множество значений ;
(Л.3) строго возрастает при , строго убывает при ;
(Л.4) при ;
при ;
(Л.5) ;
(Л.6) при ;
(Л.7) при ;
(Л.8) при ;
(Л.9) при .

Экспонента и натуральный логарифм

В определениях показательной функции и логарифма фигурирует постоянная a , которая называется основанием степени или основанием логарифма. В математическом анализе, в подавляющем большинстве случаев, получаются более простые вычисления, если в качестве основания использовать число e :
.
Показательную функцию с основанием e называют экспонентой: , а логарифм по основанию e - натуральным логарифмом: .

Свойства экспоненты и натурального логарифма изложены на страницах
«Экспонента, е в степени х »,
«Натуральный логарифм, функция ln x »

Степенная функция

Степенная функция с показателем степени p - это функция f(x) = x p , значение которой в точке x равно значению показательной функции с основанием x в точке p .
Кроме этого, f(0) = 0 p = 0 при p > 0 .

Здесь мы рассмотрим свойства степенной функции y = x p при неотрицательных значениях аргумента . Для рациональных , при нечетных m , степенная функция определена и для отрицательных x . В этом случае, ее свойства можно получить, используя четность или нечетность.
Эти случаи подробно рассмотрены и проиллюстрированы на странице «Степенная функция, ее свойства и графики ».

Теорема. Свойства степенной функции (x ≥ 0)
Степенная функция, y = x p , с показателем p имеет следующие свойства:
(С.1) определена и непрерывна на множестве
при ,
при ».

Тригонометрические функции

Теорема о непрерывности тригонометрических функций
Тригонометрические функции: синус (sin x ), косинус (cos x ), тангенс (tg x ) и котангенс (ctg x

Теорема о непрерывности обратных тригонометрических функций
Обратные тригонометрические функции: арксинус (arcsin x ), арккосинус (arccos x ), арктангенс (arctg x ) и арккотангенс (arcctg x ), непрерывны на своих областях определения.

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

На этом уроке будем учиться устанавливать непрерывность функции. Будем делать это с помощью пределов, причем односторонних - правого и левого, которые совсем не страшны, несмотря на то что записываются как и .

Но что такое вообще непрерывность функции? Пока мы не дошли до строгого определения, проще всего представить себе линию, которую можно начертить, не отрывая карандаш от бумаги. Если такая линия начерчена, то она непрерывна. Эта линия и является графиком непрерывной функции.

Графически функция непрерывна в точке , если её график не "разрывается" в этой точке. График такой непрерывной функции - показан на рисунке ниже.

Определение непрерывности функции через предел. Функция является непрерывной в точке при соблюдении трёх условий:

1. Функция определена в точке .

Если хотя бы одно из перечисленных условий не соблюдено, функция не является непрерывной в точке. При этом говорят, что функция терпит разрыв, а точки на графике, в которых график прерывается, называются точками разрыва функции. График такой функции , терпящей разрыв в точке x=2 - на рисунке ниже.

Пример 1. Функция f (x ) определена следующим образом:

Будет ли эта функция непрерывной в каждой из граничных точек её ветвей, то есть в точках x = 0 , x = 1 , x = 3 ?

Решение. Проверяем все три условия непрерывности функции в каждой граничной точке. Первое условие соблюдается, так как то, что функция определена в каждой из граничных точек, следует из определения функции. Осталось проверить остальные два условия.

Точка x = 0 . Найдём левосторонний предел в этой точке:

Найдём правосторонний предел:

x = 0 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

Как видим, предел функции и значение функции в точке x = 0 равны. Следовательно, функция является непрерывной в точке x = 0 .

Точка x = 1 . Найдём левосторонний предел в этой точке:

Найдём правосторонний предел:

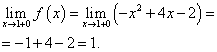
Предел функции и значение функции в точке x = 1 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

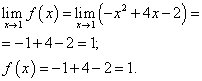Предел функции и значение функции в точке x = 1 равны. Следовательно, функция является непрерывной в точке x = 1 .

Точка x = 3 . Найдём левосторонний предел в этой точке:

Найдём правосторонний предел:

Предел функции и значение функции в точке x = 3 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

Предел функции и значение функции в точке x = 3 равны. Следовательно, функция является непрерывной в точке x = 3 .

Основной вывод: данная функция является непрерывной в каждой граничной точке.

Установить непрерывность функции в точке самостоятельно, а затем посмотреть решение

Непрерывное изменение функции можно определить как изменение постепенное, без скачков, при котором малое изменение аргумента влечёт малое изменение функции .

Проиллюстрируем это непрерывное изменение функции на примере.

Пусть над столом висит на нитке груз. Под действием этого груза нитка растягивается, поэтому расстояние l груза от точки подвеса нити является функцией массы груза m , то есть l = f (m ) , m ≥0 .

Если немного изменить массу груза, то расстояние l изменится мало: малым изменениям m соответствуют малые изменения l . Однако если масса груза близка к пределу прочности нити, то небольшое увеличение массы груза может вызвать разрыв нити: расстояние l скачкообразно увеличится и станет равным расстоянию от точки подвеса до поверхности стола. График функции l = f (m ) изображён на рисунке. На участке этот график является непрерывной (сплошной) линией, а в точке он прерывается. В результате получается график, состоящий из двух ветвей. Во всех точках, кроме , функция l = f (m ) непрерывна, а в точке она имеет разрыв.

Исследование функции на непрерывность может быть как самостоятельной задачей, так и одним из этапов полного исследования функции и построения её графика .

Непрерывность функции на промежутке

Пусть функция y = f (x ) определена в интервале ]a , b [ и непрерывна в каждой точке этого интервала. Тогда она называется непрерывной в интервале ]a , b [ . Аналогично определяется понятие непрерывности функции на промежутках вида ]- ∞, b [ , ]a , + ∞[ , ]- ∞, + ∞[ . Пусть теперь функция y = f (x ) определена на отрезке [a , b ] . Разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок. Здесь следует упомянуть о так называемой односторонней непрерывности: в точке a , оставаясь на отрезке [a , b ] , мы можем приближаться только справа, а к точке b - только слева. Функция называется непрерывной на отрезке [a , b ] , если она непрерывна во всех внутренних точках этого отрезка, непрерывна справа в точке a и непрерывна слева в точке b .

Примером непрерывной функции может служить любая из элементарных функций. Каждая элементарная функция непрерывна на любом отрезке, на котором она определена. Например, функции и непрерывны на любом отрезке [a , b ] , функция непрерывна на отрезке [0 , b ] , функция непрерывна на любом отрезке, не содержащем точку a = 2 .

Пример 4. Исследовать функцию на непрерывность.

Решение. Проверяем первое условие. Функция не определена в точках - 3 и 3. По меньшей мере одно из условий непрерывности функции на всей числовой прямой не выполняется. Поэтому данная функция является непрерывной на интервалах

Пример 5. Определить, при каком значении параметра a непрерывна на всей области определения функция

Решение.

Найдём правосторонний предел при :

Очевидно, что значение в точке x = 2 должно быть равно ax :

a = 1,5 .

Пример 6. Определить, при каких значениях параметров a и b непрерывна на всей области определения функция

Решение.
Найдём левосторонний предел функции в точке :

Следовательно, значение в точке должно быть равно 1:

Найдём левосторонний функции в точке :

Очевидно, что значение функции в точке должно быть равно :

Ответ: функция непрерывна на всей области определения при a = 1; b = -3 .

Основные свойства непрерывных функций

К понятию непрерывной функции математика пришла, изучая в первую очередь различные законы движения. Пространство и время бесконечны, и зависимость, например, пути s от времени t , выраженная законом s = f (t ) , даёт пример непрерывной функции f (t ) . Непрерывно изменяется и температура нагреваемой воды, она также является непрерывной функцией от времени: T = f (t ) .

В математическом анализе доказаны некоторые свойства, которыми обладают непрерывные функции. Приведём важнейшие из этих свойств.

1. Если непрерывная на интервале функция принимает на концах интервала значения разных знаков, то в некоторой точке этого отрезка она принимает значение, равное нулю. В более формальном изложении это свойство дано в теореме, известной как первая теорема Больцано-Коши.

2. Функция f (x ) , непрерывная на интервале [a , b ] , принимает все промежуточные значения между значениями в концевых точках, то есть, между f (a ) и f (b ) . В более формальном изложении это свойство дано в теореме, известной как вторая теорема Больцано-Коши.

Определение непрерывности функции в точке
Функция f(x) называется непрерывной в точке x 0 окрестности U(x 0) этой точки, и если предел при x стремящемся к x 0 существует и равен значению функции в x 0 :
.

Здесь подразумевается, что x 0 - это конечная точка. Значение функции в ней может быть только конечным числом.

Примеры

Пример 1

Используя определения по Гейне и Коши доказать, что функция непрерывна для всех x .

Пусть есть произвольное число. Докажем, что заданная функция непрерывна в точке . Функция определена для всех x . Поэтому она определена в точке и в любой ее окрестности.

Используем определение по Гейне

Используем . Пусть есть произвольная последовательность, сходящаяся к : . Применяя свойство предела произведения последовательностей имеем:
.
Поскольку есть произвольная последовательность, сходящаяся к , то
.
Непрерывность доказана.

Используем определение по Коши

Используем .
Рассмотрим случай . Мы вправе рассматривать функцию на любой окрестности точки . Поэтому будем считать, что
(П1.1) .

Применим формулу:
.
Учитывая (П1.1), сделаем оценку:

;
(П1.2) .

Применяя (П1.2), оценим абсолютную величину разности:
;
(П1.3) .
.
Согласно свойствам неравенств, если выполняется (П1.3), если и если , то .

Теперь рассмотрим точку . В этом случае
.
.

.
Это означает, что функция непрерывна в точке .

Аналогичным способом можно доказать, что функция , где n - натуральное число, непрерывна на всей действительной оси.

Пример 2

Используя доказать, что функция непрерывна для всех .

Заданная функция определена при . Докажем, что она непрерывна в точке .

Рассмотрим случай .
Мы вправе рассматривать функцию на любой окрестности точки . Поэтому будем считать, что
(П2.1) .

Применим формулу:
(П2.2) .
Положим . Тогда
.

Учитывая (П2.1), сделаем оценку:

.
Итак,
.

Применяя это неравенство, и используя (П2.2), оценим разность:

.
Итак,
(П2.3) .

Вводим положительные числа и , связав их соотношениями:
.
Согласно свойствам неравенств, если выполняется (П2.3), если и если , то .

Это означает, что для любого положительного всегда найдется . Тогда для всех x , удовлетворяющих неравенству , автоматически выполняется неравенство:
.
Это означает, что функция непрерывна в точке .

Теперь рассмотрим точку . Нам нужно показать, что заданная функция непрерывна в этой точке справа. В этом случае
.
Вводим положительные числа и :
.

Отсюда видно, что для любого положительного всегда найдется . Тогда для всех x , таких что , выполняется неравенство:
.
Это означает, что . То есть функция непрерывна справа в точке .

Аналогичным способом можно доказать, что функция , где n - натуральное число, непрерывна при .