Линейно зависимые и линейно независимые векторы. Линейная зависимость векторов. Базис системы векторов Являются ли векторы линейно зависимы
a 1 = { 3, 5, 1 , 4 }, a 2 = { –2, 1, -5 , -7 }, a 3 = { -1, –2, 0, –1 }.
Р е ш е н и е. Ищем общее решение системы уравнений
a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ
методом Гаусса. Для этого запишем эту однородную систему по координатам:
Матрица системы
Разрешенная система имеет вид: ![]() (r A
= 2, n
= 3). Система совместна и неопределена. Ее общее решение (x
2 – свободная переменная): x
3 = 13x
2 ; 3x
1 – 2x
2 – 13x
2 = 0 => x
1 = 5x
2 => X
o = . Наличие ненулевого частного решения, например, , говорит о том, векторы a
1 , a
2 , a
3
линейно зависимы.
(r A
= 2, n
= 3). Система совместна и неопределена. Ее общее решение (x
2 – свободная переменная): x
3 = 13x
2 ; 3x
1 – 2x
2 – 13x
2 = 0 => x
1 = 5x
2 => X
o = . Наличие ненулевого частного решения, например, , говорит о том, векторы a
1 , a
2 , a
3
линейно зависимы.
Пример 2.
Выяснить, является ли данная система векторов линейно зависимой или линейно независимой:
1. a 1 = { -20, -15, - 4 }, a 2 = { –7, -2, -4 }, a 3 = { 3, –1, –2 }.
Р е ш е н и е. Рассмотрим однородную систему уравнений a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ
или в развернутом виде (по координатам)

Система однородна. Если она невырождена, то она имеет единственное решение. В случае однородной системы – нулевое (тривиальное) решение. Значит, в этом случае система векторов независима. Если же система вырождена, то она имеет ненулевые решения и, следовательно, она зависима.
Проверяем систему на вырожденность:
 = –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.
= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.
Система невырождена и, т.о., векторы a 1 , a 2 , a 3 линейно независимы.
Задания. Выяснить, является ли данная система векторов линейно зависимой или линейно независимой:
1. a 1 = { -4, 2, 8 }, a 2 = { 14, -7, -28 }.
2. a 1 = { 2, -1, 3, 5 }, a 2 = { 6, -3, 3, 15 }.
3. a 1 = { -7, 5, 19 }, a 2 = { -5, 7 , -7 }, a 3 = { -8, 7, 14 }.
4. a 1 = { 1, 2, -2 }, a 2 = { 0, -1, 4 }, a 3 = { 2, -3, 3 }.
5. a 1 = { 1, 8 , -1 }, a 2 = { -2, 3, 3 }, a 3 = { 4, -11, 9 }.
6. a 1 = { 1, 2 , 3 }, a 2 = { 2, -1 , 1 }, a 3 = { 1, 3, 4 }.
7. a 1 = {0, 1, 1 , 0}, a 2 = {1, 1 , 3, 1}, a 3 = {1, 3, 5, 1}, a 4 = {0, 1, 1, -2}.
8. a 1 = {-1, 7, 1 , -2}, a 2 = {2, 3 , 2, 1}, a 3 = {4, 4, 4, -3}, a 4 = {1, 6, -11, 1}.
9. Доказать, что система векторов будет линейно зависимой, если она содержит:
а) два равных вектора;
б) два пропорциональных вектора.
В данной статье мы расскажем:
- что такое коллинеарные векторы;
- какие существуют условия коллинеарности векторов;
- какие существуют свойства коллинеарных векторов;
- что такое линейная зависимость коллинеарных векторов.
Коллинеарные векторы - это векторы, которые являются параллелями одной прямой или лежат на одной прямой.
Пример 1
Условия коллинеарности векторов
Два векторы являются коллинеарными, если выполняется любое из следующих условий:
- условие 1 . Векторы a и b коллинеарны при наличии такого числа λ , что a = λ b ;
- условие 2 . Векторы a и b коллинеарны при равном отношении координат:
a = (a 1 ; a 2) , b = (b 1 ; b 2) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2
- условие 3 . Векторы a и b коллинеарны при условии равенства векторного произведения и нулевого вектора:
a ∥ b ⇔ a , b = 0
Замечание 1
Условие 2 неприменимо, если одна из координат вектора равна нулю.
Замечание 2
Условие 3 применимо только к тем векторам, которые заданы в пространстве.
Примеры задач на исследование коллинеарности векторов
Пример 1Исследуем векторы а = (1 ; 3) и b = (2 ; 1) на коллинеарность.
Как решить?
В данном случае необходимо воспользоваться 2-м условием коллинеарности. Для заданных векторов оно выглядит так:
Равенство неверное. Отсюда можно сделать вывод, что векторы a и b неколлинеарны.
Ответ : a | | b
Пример 2
Какое значение m вектора a = (1 ; 2) и b = (- 1 ; m) необходимо для коллинеарности векторов?
Как решить?
Используя второе условие коллинераности, векторы будут коллинеарными, если их координаты будут пропорциональными:
Отсюда видно, что m = - 2 .
Ответ: m = - 2 .
Критерии линейной зависимости и линейной независимости систем векторов
ТеоремаСистема векторов векторного пространства линейно зависима только в том случае, когда один из векторов системы можно выразить через остальные векторы данной системы.
Доказательство
Пусть система e 1 , e 2 , . . . , e n является линейно зависимой. Запишем линейную комбинацию этой системы равную нулевому вектору:
a 1 e 1 + a 2 e 2 + . . . + a n e n = 0
в которой хотя бы один из коэффициентов комбинации не равен нулю.
Пусть a k ≠ 0 k ∈ 1 , 2 , . . . , n .
Делим обе части равенства на ненулевой коэффициент:
a k - 1 (a k - 1 a 1) e 1 + (a k - 1 a k) e k + . . . + (a k - 1 a n) e n = 0
Обозначим:
A k - 1 a m , где m ∈ 1 , 2 , . . . , k - 1 , k + 1 , n
В таком случае:
β 1 e 1 + . . . + β k - 1 e k - 1 + β k + 1 e k + 1 + . . . + β n e n = 0
или e k = (- β 1) e 1 + . . . + (- β k - 1) e k - 1 + (- β k + 1) e k + 1 + . . . + (- β n) e n
Отсюда следует, что один из векторов системы выражается через все остальные векторы системы. Что и требовалось доказать (ч.т.д.).
Достаточность
Пусть один из векторов можно линейно выразить через все остальные векторы системы:
e k = γ 1 e 1 + . . . + γ k - 1 e k - 1 + γ k + 1 e k + 1 + . . . + γ n e n
Переносим вектор e k в правую часть этого равенства:
0 = γ 1 e 1 + . . . + γ k - 1 e k - 1 - e k + γ k + 1 e k + 1 + . . . + γ n e n
Поскольку коэффициент вектора e k равен - 1 ≠ 0 , у нас получается нетривиальное представление нуля системой векторов e 1 , e 2 , . . . , e n , а это, в свою очередь, означает, что данная система векторов линейно зависима. Что и требовалось доказать (ч.т.д.).
Следствие:
- Система векторов является линейно независимой, когда ни один из ее векторов нельзя выразить через все остальные векторы системы.
- Система векторов, которая содержит нулевой вектор или два равных вектора, линейно зависима.
Свойства линейно зависимых векторов
- Для 2-х и 3-х мерных векторов выполняется условие: два линейно зависимых вектора - коллинеарны. Два коллинеарных вектора - линейно зависимы.
- Для 3-х мерных векторов выполняется условие: три линейно зависимые вектора - компланарны. (3 компланарных вектора - линейно зависимы).
- Для n-мерных векторов выполняется условие: n + 1 вектор всегда линейно зависимы.
Примеры решения задач на линейную зависимость или линейную независимость векторов
Пример 3Проверим векторы a = 3 , 4 , 5 , b = - 3 , 0 , 5 , c = 4 , 4 , 4 , d = 3 , 4 , 0 на линейную независимость.
Решение. Векторы являются линейно зависимыми, поскольку размерность векторов меньше количества векторов.
Пример 4
Проверим векторы a = 1 , 1 , 1 , b = 1 , 2 , 0 , c = 0 , - 1 , 1 на линейную независимость.
Решение. Находим значения коэффициентов, при которых линейная комбинация будет равняться нулевому вектору:
x 1 a + x 2 b + x 3 c 1 = 0
Записываем векторное уравнение в виде линейного:
x 1 + x 2 = 0 x 1 + 2 x 2 - x 3 = 0 x 1 + x 3 = 0
Решаем эту систему при помощи метода Гаусса:
1 1 0 | 0 1 2 - 1 | 0 1 0 1 | 0 ~
Из 2-ой строки вычитаем 1-ю, из 3-ей - 1-ю:
~ 1 1 0 | 0 1 - 1 2 - 1 - 1 - 0 | 0 - 0 1 - 1 0 - 1 1 - 0 | 0 - 0 ~ 1 1 0 | 0 0 1 - 1 | 0 0 - 1 1 | 0 ~
Из 1-й строки вычитаем 2-ю, к 3-ей прибавляем 2-ю:
~ 1 - 0 1 - 1 0 - (- 1) | 0 - 0 0 1 - 1 | 0 0 + 0 - 1 + 1 1 + (- 1) | 0 + 0 ~ 0 1 0 | 1 0 1 - 1 | 0 0 0 0 | 0
Из решения следует, что у системы множество решений. Это значит, что существует ненулевая комбинация значения таких чисел x 1 , x 2 , x 3 , при которых линейная комбинация a , b , c равняется нулевому вектору. Следовательно, векторы a , b , c являются линейно зависимыми.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Введенные нами линейные операции над векторами дают возможность составлять различные выражения для векторных величин и преобразовывать их при помощи установленных для этих операций свойств.
Исходя из заданного набора векторов а 1 , ..., а n , можно составить выражение вида
где а 1 , ..., а n - произвольные действительные числа. Это выражение называют линейной комбинацией векторов а 1 , ..., а n . Числа α i , i = 1, n , представляют собой коэффициенты линейной комбинации . Набор векторов называют еще системой векторов .
В связи с введенным понятием линейной комбинации векторов возникает задача описания множества векторов, которые могут быть записаны в виде линейной комбинации данной системы векторов а 1 , ..., а n . Кроме того, закономерны вопросы об условиях, при которых существует представление вектора в виде линейной комбинации, и о единственности такого представления.
Определение 2.1. Векторы а 1 , ..., а n называют линейно зависимыми , если существует такой набор коэффициентов α 1 , ... , α n , что
α 1 a 1 + ... + α n а n = 0 (2.2)
и при этом хотя бы один из этих коэффициентов ненулевой. Если указанного набора коэффициентов не существует, то векторы называют линейно независимыми .
Если α 1 = ... = α n = 0, то, очевидно, α 1 а 1 + ... + α n а n = 0. Имея это в виду, можем сказать так: векторы а 1 , ..., а n линейно независимы, если из равенства (2.2) вытекает, что все коэффициенты α 1 , ... , α n равны нулю.
Следующая теорема поясняет, почему новое понятие названо термином "зависимость" (или "независимость"), и дает простой критерий линейной зависимости.
Теорема 2.1. Для того чтобы векторы а 1 , ..., а n , n > 1, были линейно зависимы, необходимо и достаточно, чтобы один из них являлся линейной комбинацией остальных.
◄ Необходимость. Предположим, что векторы а 1 , ..., а n линейно зависимы. Согласно определению 2.1 линейной зависимости, в равенстве (2.2) слева есть хотя бы один ненулевой коэффициент, например α 1 . Оставив первое слагаемое в левой части равенства, перенесем остальные в правую часть, меняя, как обычно, у них знаки. Разделив полученное равенство на α 1 , получим
a 1 =-α 2 /α 1 ⋅ a 2 - ... - α n /α 1 ⋅ a n
т.е. представление вектора a 1 в виде линейной комбинации остальных векторов а 2 , ..., а n .
Достаточность. Пусть, например, первый вектор а 1 можно представить в виде линейной комбинации остальных векторов: а 1 = β 2 а 2 + ... + β n а n . Перенеся все слагаемые из правой части в левую, получим а 1 - β 2 а 2 - ... - β n а n = 0, т.е. линейную комбинацию векторов а 1 , ..., а n с коэффициентами α 1 = 1, α 2 = - β 2 , ..., α n = - β n , равную нулевому вектору. В этой линейной комбинации не все коэффициенты равны нулю. Согласно определению 2.1, векторы а 1 , ..., а n линейно зависимы.
Определение и критерий линейной зависимости сформулированы так, что подразумевают наличие двух или более векторов. Однако можно также говорить о линейной зависимости одного вектора. Чтобы реализовать такую возможность, нужно вместо "векторы линейно зависимы" говорить "система векторов линейно зависима". Нетрудно убедиться, что выражение "система из одного вектора линейно зависима" означает, что этот единственный вектор является нулевым (в линейной комбинации имеется только один коэффициент, и он не должен равняться нулю).
Понятие линейной зависимости имеет простую геометрическую интерпретацию. Эту ин-терпретацию проясняют следующие три утверждения.
Теорема 2.2. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
◄ Если векторы а и b линейно зависимы, то один из них, например а, выражается через другой, т.е. а = λb для некоторого действительного числа λ. Согласно определению 1.7 произведения вектора на число, векторы а и b являются коллинеарными.
Пусть теперь векторы а и b коллинеарны. Если они оба нулевые, то очевидно, что они линейно зависимы, так как любая их линейная комбинация равна нулевому вектору. Пусть один из этих векторов не равен 0, например вектор b. Обозначим через λ отношение длин векторов: λ = |а|/|b|. Коллинеарные векторы могут быть однонаправленными или противоположно направленными . В последнем случае у λ изменим знак. Тогда, проверяя определение 1.7, убеждаемся, что а = λb. Согласно теореме 2.1, векторы а и b линейно зависимы.
Замечание 2.1. В случае двух векторов, учитывая критерий линейной зависимости, доказанную теорему можно переформулировать так: два вектора коллинеарны тогда и только тогда, когда один из них представляется как произведение другого на число. Это является удобным критерием коллинеарности двух векторов.
Теорема 2.3. Три вектора линейно зависимы тогда и только тогда, когда они компланарны .
◄ Если три вектора а, Ь, с линейно зависимы, то, согласно теореме 2.1, один из них, например а, является линейной комбинацией остальных: а = βb + γс. Совместим начала векторов b и с в точке A. Тогда векторы βb, γс будут иметь общее начало в точке A и по правилу параллелограмма их сумма, т.е. вектор а, будет представлять собой вектор с началом A и концом , являющимся вершиной параллелограмма, построенного на векторах-слагаемых. Таким образом, все векторы лежат в одной плоскости, т. е. компланарны.
Пусть векторы а, b, с компланарны. Если один из этих векторов является нулевым, то очевидно, что он будет линейной комбинацией остальных. Достаточно все коэффициенты линейной комбинации взять равными нулю. Поэтому можно считать, что все три вектора не являются нулевыми. Совместим начала этих векторов в общей точке O. Пусть их концами будут соот-ветственно точки A, B, C (рис. 2.1). Через точку C проведем прямые, параллельные прямым, проходящим через пары точек O, A и O, B. Обозначив точки пересечения через A" и B", получим параллелограмм OA"CB", следовательно, OC" = OA" + OB" . Вектор OA" и ненулевой вектор а= OA коллинеарны, а потому первый из них может быть получен умножением второго на действительное число α:OA" = αOA . Аналогично OB" = βOB , β ∈ R. В результате получаем,что OC" = α OA + βOB , т.е. вектор с является линейной комбинацией векторов а и b. Согласно теореме 2.1, векторы a, b, с являются линейно зависимыми.

Теорема 2.4. Любые четыре вектора линейно зависимы.
◄ Доказательство проводим по той же схеме, что и в теореме 2.3. Рассмотрим произвольные четыре вектора a, b, с и d. Если один из четырех векторов является нулевым, либо среди них есть два коллинеарных вектора, либо три из четырех векторов компланарны, то эти четыре вектора линейно зависимы. Например, если векторы а и b коллинеарны, то мы можем составить их линейную комбинацию αa + βb = 0 с ненулевыми коэффициентами, а затем в эту комбинацию добавить оставшиеся два вектора, взяв в качестве коэффициентов нули. Получим равную 0 линейную комбинацию четырех векторов, в которой есть ненулевые коэффициенты.
Таким образом, мы можем считать, что среди выбранных четырех векторов нет нулевых, никакие два не коллинеарны и никакие три не являются компланарными. Выберем в качестве их общего начала точку О. Тогда концами векторов a, b, с, d будут некоторые точки A, B, С, D (рис. 2.2). Через точку D проведем три плоскости, параллельные плоскостям ОВС, OCA, OAB, и пусть A", B", С" - точки пересечения этих плоскостей с прямыми OA, OB, ОС соответственно. Мы получаем параллелепипед OA"C"B"C"B"DA", и векторы a, b, с лежат на его ребрах, выходящих из вершины О. Так как четырехугольник OC"DC" является параллелограммом, то OD = OC" + OC" . В свою очередь, отрезок ОС" является диагональю параллелограмма OA"C"B", так что OC" = OA" + OB" , а OD = OA" + OB" + OC" .

Остается заметить, что пары векторов OA ≠ 0 и OA" , OB ≠ 0 и OB" , OC ≠ 0 и OC" коллинеарны, и, следовательно, можно подобрать коэффициенты α, β, γ так, что OA" = αOA , OB" = βOB и OC" = γOC . Окончательно получаем OD = αOA + βOB + γOC . Следовательно, вектор OD выражается через остальные три вектора, а все четыре вектора, согласно теореме 2.1, линейно зависимы.
Пусть в -мерном арифметическом пространстве имеется совокупность векторов  .
.
Определение 2.1.
Совокупность векторов  называется линейно независимой
системой векторов, если равенство вида
называется линейно независимой
системой векторов, если равенство вида
выполняется только при нулевых значениях числовых параметров  .
.
Если равенство (2.1) может быть выполнено при условии, что хотя бы один из коэффициентов отличен от нуля, то такая система векторов будет называться линейно зависимой .
Пример 2.1. Проверить линейную независимость векторов



Решение. Составим равенство вида (2.1)
Левая часть данного выражения может обращаться в нуль только при выполнении условия  , которое означает, что система является линейно-независимой.
, которое означает, что система является линейно-независимой.
Пример 2.1.
Будут ли векторы 
 линейно независимыми?
линейно независимыми?
Решение.
Нетрудно проверить, что равенство верно при значениях  ,
,  . Значит, данная система векторов линейно зависима.
. Значит, данная система векторов линейно зависима.
Теорема 2.1. Если система векторов является линейно зависимой, то любой вектор из этой системы может быть представлен в виде линейной комбинации (или суперпозиции) остальных векторов системы.
Доказательство
. Предположим, что система векторов  линейно зависима. Тогда в силу определения существует набор чисел
линейно зависима. Тогда в силу определения существует набор чисел  , среди которых хотя бы одно число отлично от нуля, и при этом справедливо равенство (2.1):
, среди которых хотя бы одно число отлично от нуля, и при этом справедливо равенство (2.1):
Без потери общности предположим, что ненулевым коэффициентом является , то есть  . Тогда последнее равенство можно разделить на и далее выразить вектор :
. Тогда последнее равенство можно разделить на и далее выразить вектор :
 .
.
Таким образом, вектор представлен в виде суперпозиции векторов  . Теорема 1 доказана.
. Теорема 1 доказана.
Следствие.
Если  – совокупность линейно независимых векторов, то ни один вектор из этого набора не может быть выражен через остальные
.
– совокупность линейно независимых векторов, то ни один вектор из этого набора не может быть выражен через остальные
.
Теорема 2.2.
Если система векторов
 содержит ноль-вектор, то такая система обязательно будет линейно зависимой
.
содержит ноль-вектор, то такая система обязательно будет линейно зависимой
.
Доказательство
. Пусть вектор является ноль-вектором, то есть  .
.
Тогда выбираем постоянные ( ) следующим образом:
) следующим образом:
 , .
, .
При этом равенство (2.1) выполняется. Первое слагаемое слева равно нулю вследствие того, что – ноль-вектор. Остальные слагаемые обращаются в нуль, будучи умноженными на нулевые константы ( ). Таким образом,
). Таким образом,
при  , а значит, векторы
, а значит, векторы  линейно зависимые. Теорема 2.2 доказана.
линейно зависимые. Теорема 2.2 доказана.
Следующий вопрос, на который нам предстоит ответить, какое наибольшее количество векторов может составить линейно независимую систему в n -мерном арифметическом пространстве. В пункте 2.1 был рассмотрен естественный базис (1.4):

Было установлено, что произвольный вектор -мерного пространства является линейной комбинацией векторов естественного базиса, то есть произвольный вектор  выражается в естественном базисе в виде
выражается в естественном базисе в виде
 , (2.2)
, (2.2)
где – координаты вектора , представляющие собой некоторые числа. Тогда равенство

возможно лишь при , а значит, векторов  естественного базиса образуют линейно независимую систему. Если добавить к этой системе произвольный вектор
естественного базиса образуют линейно независимую систему. Если добавить к этой системе произвольный вектор  , то на основании следствия теоремы 1 система будет зависимой, поскольку вектор выражается через векторы
, то на основании следствия теоремы 1 система будет зависимой, поскольку вектор выражается через векторы  по формуле (2.2).
по формуле (2.2).
Этот пример показывает, что в n -мерном арифметическом пространстве существуют системы, состоящие из линейно независимых векторов. А если к этой системе добавить хотя бы один вектор, то получим систему линейно зависимых векторов. Докажем, что если число векторов превышает размерность пространства, то они линейно зависимые.
Теорема 2.3. В -мерном арифметическом пространстве не существует системы, состоящей более чем из линейно независимых векторов.
Доказательство . Рассмотрим произвольных -мерных векторов:
………………………
Пусть  . Составим линейную комбинацию векторов (2.3) и приравняем её к нулю:
. Составим линейную комбинацию векторов (2.3) и приравняем её к нулю:
Векторное равенство (2.4) равносильно скалярным равенствам для координат  векторов
векторов  :
:
 (2.5)
(2.5)
Эти равенства образуют систему однородных уравнений с неизвестными  . Так как число неизвестных больше числа уравнений (
. Так как число неизвестных больше числа уравнений ( ), то в силу следствия теоремы 9.3 раздела 1 однородная система (2.5) имеет ненулевое решение. Следовательно, равенство (2.4) справедливо при некоторых значениях
), то в силу следствия теоремы 9.3 раздела 1 однородная система (2.5) имеет ненулевое решение. Следовательно, равенство (2.4) справедливо при некоторых значениях  , среди которых не все равны нулю, а значит, система векторов (2.3) линейно зависимая. Теорема 2.3 доказана.
, среди которых не все равны нулю, а значит, система векторов (2.3) линейно зависимая. Теорема 2.3 доказана.
Следствие. В -мерном пространстве существуют системы, состоящие из линейно независимых векторов, а любая система, содержащая больше чем векторов, будет линейно зависимой.
Определение 2.2. Систему линейно независимых векторов называют базисом пространства , если любой вектор пространства может быть выражен в виде линейной комбинации этих линейно независимых векторов.
2.3. Линейное преобразование векторов
Рассмотрим два вектора и -мерного арифметического пространства .
Определение 3.1.
Если каждому вектору  сопоставлен вектор из этого же пространства , то говорят, что задано некоторое преобразование -мерного арифметического пространства.
сопоставлен вектор из этого же пространства , то говорят, что задано некоторое преобразование -мерного арифметического пространства.
Будем обозначать это преобразование через . Вектор будем называть образом . Можно записать равенсто
 . (3.1)
. (3.1)
Определение 3.2. Преобразование (3.1) будем называть линейным, если оно удовлетворяет следующим свойствам:
, (3.2)
 ,
(3.3)
,
(3.3)
где - произвольный скаляр (число).
Зададим преобразование (3.1) в координатной форме. Пусть координаты векторов  и
и  связаны зависимостью
связаны зависимостью
 (3.4)
(3.4)
Формулы (3.4) задают преобразование (3.1) в координатной форме. Коэффициенты ( ) системы равенств (3.4) можно представить в виде матрицы
) системы равенств (3.4) можно представить в виде матрицы

называемой матрицей преобразования (3.1).
Введём векторы-столбцы
 ,
,
элементы которых суть координаты векторов  и
и  соответственно, так что
соответственно, так что  и
и  . Будем далее векторы-столбцы и называть векторами.
. Будем далее векторы-столбцы и называть векторами.
Тогда преобразование (3.4) может быть записано в матричной форме
 . (3.5)
. (3.5)
Преобразование (3.5) является линейным в силу свойств арифметических операций над матрицами .
Рассмотрим некоторое преобразование , образом которого является ноль-вектор. В матричном виде это преобразование будет иметь вид
 , (3.6)
, (3.6)
а в координатной форме – представлять собой систему линейных однородных уравнений
 (3.7)
(3.7)
Определение 3.3.
Линейное преобразование называется невырожденным, если определитель матрицы линейного преобразования не равен нулю, то есть  . Если определитель обращается в нуль, то преобразование будет вырожденным
. Если определитель обращается в нуль, то преобразование будет вырожденным  .
.
Известно, что система (3.7) имеет тривиальное (очевидное) решение – нулевое. Это решение является единственным, если только определитель матрицы не равен нулю.
Ненулевые решения системы (3.7) могут появляться, если линейное преобразование является вырожденным, то есть при нулевом определителе матрицы .
Определение 3.4. Рангом преобразования (3.5) называется ранг матрицы преобразования .
Можно сказать, что этому же числу равно количество линейно-независимых строк матрицы .
Обратимся к геометрической интерпретации линейного преобразования (3.5).
Пример 3.1.
Пусть задана матрица линейного преобразования  , где
, где  Возьмем произвольный вектор
Возьмем произвольный вектор  , где
, где  и найдем его образ:
и найдем его образ:  Тогда вектор
Тогда вектор  .
.
Если  , то вектор изменит и длину и направление. На рис.1
, то вектор изменит и длину и направление. На рис.1  .
.
Если  , то получим образ
, то получим образ
 ,
,
то есть вектор  или
или  , а это значит, что изменит только длину, но не изменит направление (рис. 2).
, а это значит, что изменит только длину, но не изменит направление (рис. 2).
Пример 3.2.
Пусть  ,
,  . Найдём образ:
. Найдём образ:
 ,
,
то есть  , или
, или  .
.
Вектор  в результате преобразования изменил своё направление на противоположное, при этом длина вектора сохранилась (рис. 3).
в результате преобразования изменил своё направление на противоположное, при этом длина вектора сохранилась (рис. 3).
Пример 3.3.
Рассмотрим матрицу  линейного преобразования. Несложно показать, что в этом случае образ вектора полностью совпадает с самим вектором (рис. 4). Действительно,
линейного преобразования. Несложно показать, что в этом случае образ вектора полностью совпадает с самим вектором (рис. 4). Действительно,
 .
.
Можно сказать, что линейное преобразование векторов изменяет исходный вектор  и по длине, и по направлению. Однако в некоторых случаях существуют такие матрицы, которые преобразуют вектор только по направлению (пример 3.2) или только по длине (пример 3.1, случай
и по длине, и по направлению. Однако в некоторых случаях существуют такие матрицы, которые преобразуют вектор только по направлению (пример 3.2) или только по длине (пример 3.1, случай  ).
).
Следует заметить, что все векторы, лежащие на одной прямой, образуют систему линейно зависимых векторов.
Вернёмся к линейному преобразованию (3.5)

и рассмотрим совокупность векторов  , для которых образом является нуль-вектор, так что
, для которых образом является нуль-вектор, так что  .
.
Определение 3.5
. Совокупность векторов , являющихся решением уравнения  , образует подпространство -мерного арифметического пространства и называется ядром линейного преобразования
.
, образует подпространство -мерного арифметического пространства и называется ядром линейного преобразования
.
Определение 3.6. Дефектом линейного преобразования
называется размерность ядра этого преобразования, то есть, наибольшее число линейно-независимых векторов , удовлетворяющих уравнению  .
.
Так как рангом линейного преобразования мы называем ранг матрицы , то можно сформулировать следующее утверждение относительно дефекта матрицы: дефект равен разности ![]() , где – размерность матрицы, – её ранг.
, где – размерность матрицы, – её ранг.
Если ранг матрицы линейного преобразования (3.5) ищется методом Гаусса, то ранг совпадает с количеством отличных от нуля элементов на главной диагонали уже преобразованной матрицы, а дефект определяется количеством нулевых строк.
Если линейное преобразование является невырожденным, то есть  , то его дефект обращается в ноль, поскольку ядром является единственный нулевой вектор.
, то его дефект обращается в ноль, поскольку ядром является единственный нулевой вектор.
Если линейное преобразование вырожденное и  , то система (3.6) кроме нулевого решения имеет другие, и дефект в этом случае уже отличен от нуля.
, то система (3.6) кроме нулевого решения имеет другие, и дефект в этом случае уже отличен от нуля.
Особый интерес вызывают преобразования, которые, меняя длину, не меняют направление вектора. Точнее говоря, оставляют вектор на прямой, содержащей исходный вектор, при условии, что прямая проходит через начало координат. Такие преобразования будут рассмотрены в следующем пункте 2.4.
Выражение вида называется линейной комбинацией векторов A 1 , A 2 ,...,A n с коэффициентами λ 1, λ 2 ,...,λ n .
Определение линейной зависимости системы векторов
Система векторов A 1 , A 2 ,...,A n называется линейно зависимой , если существует ненулевой набор чисел λ 1, λ 2 ,...,λ n , при котором линейная комбинация векторов λ 1 *A 1 +λ 2 *A 2 +...+λ n *A n равна нулевому вектору , то есть система уравнений: имеет ненулевое решение.
Набор чисел λ 1, λ 2 ,...,λ n является ненулевым, если хотя бы одно из чисел λ 1, λ 2 ,...,λ n отлично от нуля.
Определение линейной независимости системы векторов
Пример 29.1Система векторов A 1 , A 2 ,...,A n называется линейно независимой , если линейная комбинация этих векторов λ 1 *A 1 +λ 2 *A 2 +...+λ n *A n равна нулевому вектору только при нулевом наборе чисел λ 1, λ 2 ,...,λ n , то есть система уравнений: A 1 x 1 +A 2 x 2 +...+A n x n =Θ имеет единственное нулевое решение.
Проверить, является ли линейно зависимой система векторов
Решение :

1. Составляем систему уравнений :
2. Решаем ее методом Гаусса . Преобразования Жордано системы приведены в таблице 29.1. При расчете правые части системы не записываются так как они равны нулю и при преобразованиях Жордана не изменяются.

3. Из последних трех строк таблицы записываем разрешенную систему, равносильную исходной системе:
![]()
4. Получаем общее решение системы :
5. Задав по своему усмотрению значение свободной переменной x 3 =1, получаем частное ненулевое решение X=(-3,2,1).
Ответ: Таким образом, при ненулевом наборе чисел (-3,2,1) линейная комбинация векторов равняется нулевому вектору -3A 1 +2A 2 +1A 3 =Θ. Следовательно, система векторов линейно зависимая .
Свойства систем векторов
Свойство (1)
Если система векторов линейно зависимая, то хотя бы один из векторов разлагается по остальным и, наоборот, если хотя бы один из векторов системы разлагается по остальным, то система векторов линейно зависимая.
Свойство (2)
Если какая-либо подсистема векторов линейно зависимая, то и вся система линейно зависимая.
Свойство (3)
Если система векторов линейно независимая, то любая ее подсистема линейно независимая.
Свойство (4)
Любая система векторов, содержащая нулевой вектор, линейно зависимая.
Свойство (5)
Система m-мерных векторов всегда является линейно зависимой, если число векторов n больше их размерности (n>m)
Базис системы векторов
Базисом системы векторов A 1 , A 2 ,..., A n называется такая подсистема B 1 , B 2 ,...,B r (каждый из векторов B 1 ,B 2 ,...,B r является одним из векторов A 1 , A 2 ,..., A n) , которая удовлетворяет следующим условиям:
1. B 1 ,B 2 ,...,B r линейно независимая система векторов;
2. любой вектор A j системы A 1 , A 2 ,..., A n линейно выражается через векторы B 1 ,B 2 ,...,B rr — число векторов входящих в базис.
Теорема 29.1 О единичном базисе системы векторов.Если система m-мерных векторов содержит m различных единичных векторов E 1 E 2 ,..., E m , то они образуют базис системы.
Алгоритм нахождения базиса системы векторов
Для того, чтобы найти базис системы векторов A 1 ,A 2 ,...,A n необходимо:
- Составить соответствующую системе векторов однородную систему уравнений A 1 x 1 +A 2 x 2 +...+A n x n =Θ
- Привести эту систему
 Милосердие, сострадание — аргументы ЕГЭ
Милосердие, сострадание — аргументы ЕГЭ Русские священники на войне
Русские священники на войне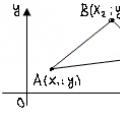 Расстояние от точки до точки, формулы, примеры, решения
Расстояние от точки до точки, формулы, примеры, решения